Программа Решения Транспортной Задачи
НЕГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ СРЕДНЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ 'ЭКОНОМИКО-КОМПЬЮТЕРНЫЙ ТЕХНИКУМ' ГРАФИЧЕСКАЯ КУРСОВАЯ РАБОТА по дисциплине: 'Математические методы' на тему: ' Транспортная задача' Выполнил: студент 4-го курса группы 08-1 (п) Лагутин Р.И. Руководитель: Ходаковская Т.Ю. Курск – 2010 г. Задание Цели работы: изучить методы решения транспортной задачи и их реализацию при решении практической задачи. Задания:. Рассмотреть понятие транспортной задачи, ее типы. Рассмотреть различные методы решения транспортной задачи.
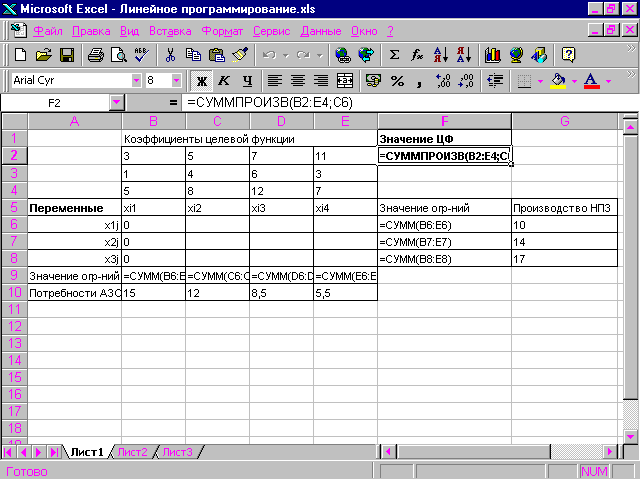
Построить первый опорный план данной транспортной задачи двумя различными методами. Найти оптимальный план перевозок данной задачи методом потенциалов. Решить данную задачу с использованием MS Excel (привести описание решения). Составьте компьютерную программу по решению задач данного типа (привести описание программы, приложить программу в электронном виде). На четырех складах фирмы находится 70, 30, 40 и 60 холодильников соответственно, которые следует доставить в четыре магазина фирмы в количестве 50, 70, 40 и 40 холодильников в каждый из магазинов. Стоимости перевозки одного холодильника с первого склада в каждый из магазинов составляют 6, 4, 9 и 7 денежных единиц соответственно, со второго склада - 7, 2, 5 и 6 денежных единиц, с третьего склада - 2, 6, 3 и 3 денежных единиц, с четвертого склада - 3, 3, 6 и 5 денежных единиц соответственно.
Исследование и характеристика особенностей транспортной задачи, которая является. Транспортная программа для автоматизации транспортного предприятия и решения.
Программа Для Решения Транспортной Задачи Скачать Бесплатно
Определить план перевозок холодильников со складов в магазины, при котором общие затраты на перевозку были бы наименьшими. Оглавление Задание Введение Транспортная задача Математическая модель Опорный план Распределительный метод оптимального плана Решение транспортной задачи методом потенциалов Всякий потенциальный план является оптимальным Заключение Список используемой литературы Введение Каждый человек ежедневно, не всегда осознавая это, решает проблему: как получить наибольший эффект, обладая ограниченными средствами. Наши средства и ресурсы всегда ограничены. Жизнь была бы менее интересной, если бы это было не так. Не трудно выиграть сражение, имея армию в 10 раз большую, чем у противника. Чтобы достичь наибольшего эффекта, имея ограниченные средства, надо составить план, или программу действий.
Раньше план в таких случаях составлялся “на глазок”. В середине XX века был создан специальный математический аппарат, помогающий это делать “по науке”. Соответствующий раздел математики называется математическим программированием. Слово “программирование' здесь и в аналогичных терминах (“линейное программирование, динамическое программирование” и т.п.) обязано отчасти историческому недоразумению, отчасти неточному переводу с английского. По-русски лучше было бы употребить слово “планирование”. С программированием для ЭВМ математическое программирование имеет лишь то общее, что большинство возникающих на практике задач математического программирования слишком громоздки для ручного счета, решить их можно только с помощью ЭВМ, предварительно составив программу. Временем рождения линейного программирования принято считать 1939 г., когда была напечатана брошюра Леонида Витальевича Канторовича “Математические методы организации и планирования производства”.
Под названием “транспортная задача” объединяется широкий круг задач с единой математической моделью. Данные задачи относятся к задачам линейного программирования и могут быть решены симплексным методом. Однако матрица системы ограничений транспортной задачи настолько своеобразна, что для ее решения разработаны специальные методы. Эти методы, как и симплексный метод, позволяют найти начальное опорное решение, а затем, улучшая его, получить оптимальное решение. Целью транспортной задачи является обеспечение получения (доставки) продукции (товара) потребителю в нужное время и место при минимально возможных совокупных затратах трудовых, материальных, финансовых ресурсов. Цель транспортной деятельности считается достигнутой при выполнении шести условий:.
нужный товар;. необходимого качества;. в необходимом количестве доставлен;. в нужное время;. в нужное место;.
с минимальными затратами. Объектом изучения являются материальные и соответствующие им финансовые, информационные потоки, сопровождающие производственно-коммерческую деятельность. В данной курсовой работе будут рассмотрены понятие транспортной задачи, ее типы, различные методы решения. Решена задача по заданию 4.1 с помощью MS Excel и приложена компьютерная программа по решению задачи данного типа. Транспортная задача Линейные транспортные задачи составляют особый класс задач линейного программирования. Задача заключается в отыскании такого плана перевозок продукции с m складов в пункт назначения n который, потребовал бы минимальных затрат.
Если потребитель j получает единицу продукции (по прямой дороге) со склада i, то возникают издержки С ij. Предполагается, что транспортные расходы пропорциональны перевозимому количеству продукции, т.е. Перевозка k единиц продукции вызывает расходы k С i j. Далее, где a i есть количество продукции, находящееся на складе i, и b j - потребность потребителя j. Если сумма запасов в пунктах отправления превышает сумму поданных заявок то количество продукции, равное остается на складах. В этом случае мы введем 'фиктивного' потребителя n +1 с потребностью и положим транспортные расходы p i,n +1 равными 0 для всех i.
Если сумма поданных заявок превышает наличные запасы то потребность не может быть покрыта. Эту задачу можно свести к обычной транспортной задаче с правильным балансом, если ввести фиктивный пункт отправления m + 1 с запасом и стоимость перевозок из фиктивного пункта отправления во все пункты назначения принять равным нулю. Математическая модель где x ij количество продукции, поставляемое со склада i потребителю j, а С i j издержки (стоимость перевозок со склада i потребителю j).
Опорный план Решение транспортной задачи начинается с нахождения опорного плана. Для этого существуют различные способы.
Например, способ северо-западного угла, способ минимальной стоимости по строке, способ минимальной стоимости по столбцу и способ минимальной стоимости таблицы. Рассмотрим простейший, так называемый способ северо-западного угла.

Пояснить его проще всего будет на конкретном примере: Условия транспортной задачи заданы транспортной таблицей. Таблица № 1 ПН ПО В 1 В 2 В 3 В 4 В 5 Запасы а i А 1 10 8 5 6 9 48 А 2 6 7 8 6 5 30 А 3 8 7 10 8 7 27 А 4 7 5 4 6 8 20 Заявки b j 18 27 42 12 26 125 Будем заполнять таблицу перевозками постепенно начиная с левой верхней ячейки ('северо-западного угла' таблицы). Будем рассуждать при этом следующим образом.
Пункт В 1 подал заявку на 18 единиц груза. Удовлетворим эту заявку за счёт запаса 48, имеющегося в пункте А 1, и запишем перевозку 18 в клетке (1,1). После этого заявка пункта В 1 удовлетворена, а в пункте А 1 осталось ещё 30 единиц груза. Удовлетворим за счёт них заявку пункта В 2 (27 единиц), запишем 27 в клетке (1,2); оставшиеся 3 единицы пункта А 1 назначим пункту В 3. В составе заявки пункта В 3 остались неудовлетворёнными 39 единиц. Из них 30 покроем за счёт пункта А 2, чем его запас будет исчерпан, и ещё 9 возьмём из пункта А 3.
Из оставшихся 18 единиц пункта А 3 12 выделим пункту В 4; оставшиеся 6 единиц назначим пункту В 5, что вместе со всеми 20 единицами пункта А 4 покроет его заявку. На этом распределение запасов закончено; каждый пункт назначения получил груз, согласно своей заявки.
Это выражается в том, что сумма перевозок в каждой строке равна соответствующему запасу, а в столбце - заявке. Таким образом, нами сразу же составлен план перевозок, удовлетворяющий балансовым условиям. Полученное решение является опорным решением транспортной задачи: Таблица № 2 ПН ПО В 1 В 2 В 3 В 4 В 5 Запасы а i А 1 10 18 8 27 5 3 6 9 48 А 2 6 7 8 30 6 5 30 А 3 8 7 10 9 8 12 7 6 27 А 4 7 5 4 6 8 20 20 Заявки b j 18 27 42 12 26 125 Составленный нами план перевозок, не является оптимальным по стоимости, так как при его построении мы совсем не учитывали стоимость перевозок С ij. Другой способ - способ минимальной стоимости по строке - основан на том, что мы распределяем продукцию от пункта A i не в любой из пунктов B j, а в тот, к которому стоимость перевозки минимальна.
Программа Решения Транспортной Задачи
Если в этом пункте заявка полностью удовлетворена, то мы убираем его из расчетов и находим минимальную стоимость перевозки из оставшихся пунктов B j. Во всем остальном этот метод схож с методом северо-западного угла. В результате, опорный план, составленный способом минимальной стоимости по строке выглядит, так как показано в таблице № 3. При этом методе может получиться, что стоимости перевозок C ij и C ik от пункта A i к пунктам B j и B k равны. В этом случае, с экономической точки зрения, выгоднее распределить продукцию в тот пункт, в котором заявка больше. Так, например, в строке 2: C 21 = C 24, но заявка b 1 больше заявки b 4, поэтому 4 единицы продукции мы распределим в клетку (2,1).
Таблица № 3 ПН ПО В 1 В 2 В 3 В 4 В 5 Запасы а i А 1 10 8 5 42 6 6 9 48 А 2 6 4 7 8 6 5 26 30 А 3 8 7 27 10 8 7 0 27 А 4 7 14 5 4 6 6 8 20 Заявки b j 18 27 42 12 26 125 Способ минимальной стоимости по столбцу аналогичен предыдущему способу. Их отличие состоит в том, что во втором способе мы распределяем продукцию от пунктов B i к пунктам A j по минимальной стоимости C ji. Опорный план, составленный способами минимальных стоимостей, обычно более близок к оптимальному решению. Так в нашем примере общие затраты на транспортировку по плану, составленному первым способом F 0 = 1039, а по второму F 0 = 723. Клетки таблицы, в которых стоят ненулевые перевозки, являются базисными. Их число должно равняться m + n - 1.
Необходимо отметить также, что встречаются такие ситуации, когда количество базисных клеток меньше чем m + n - 1. В этом случае распределительная задача называется вырожденной. И следует в одной из свободных клеток поставить количество перевозок равное нулю. Так, например, в таблице № 3: m + n - 1 = 4 + 5 - 1 = 8, а базисных клеток 7, поэтому нужно в одну из клеток строки 3 или столбца 2 поставить значение “0”. Например в клетку (3,5). Составляя план по способам минимальных стоимостей в отличии от плана по способу северо-западного угла мы учитываем стоимости перевозок C ij, но все же не можем утверждать, что составленный нами план является оптимальным.
Распределительный метод оптимального плана Теперь попробуем улучшить план, составленный способом северо-западного угла. Перенесем, например, 18 единиц из клетки (1,1) в клетку (2,1) и чтобы не нарушить баланса перенесём те же 18 единиц из клетки (2,3) в клетку (1,3). Получим новый план. Подсчитав стоимость опорного плана (она ровняется 1039) и стоимость нового плана (она ровняется 913) нетрудно убедиться, что стоимость нового плана на 126 единиц меньше. Таким образом, за счёт циклической перестановки 18 единиц груза из одних клеток в другие нам удалось понизить стоимость плана: Таблица №4 ПН ПО В 1 В 2 В 3 В 4 В 5 Запасы а i А 1 10 8 27 5 21 6 9 48 А 2 6 18 7 8 12 6 5 30 А 3 8 7 10 9 8 12 7 6 27 А 4 7 5 4 6 8 20 20 Заявки b j 18 27 42 12 26 125 На этом способе уменьшения стоимости в дальнейшем и будет основан алгоритм оптимизации плана перевозок. Циклом в транспортной задаче мы будем называть несколько занятых клеток, соединённых замкнутой, ломанной линией, которая в каждой клетке совершает поворот на 90°. Существует несколько вариантов цикла: 1.) 2.) 3.) Нетрудно убедиться, что каждый цикл имеет чётное число вершин и значит, чётное число звеньев (стрелок).
Условимся отмечать знаком + те вершины цикла, в которых перевозки необходимо увеличить, а знаком -, те вершины, в которых перевозки необходимо уменьшить. Цикл с отмеченными вершинами будем называть означенным. Перенести какое-то количество единиц груза по означенному циклу, это значит увеличить перевозки, стоящие в положительных вершинах цикла, на это количество единиц, а перевозки, стоящие в отрицательных вершинах уменьшить на то же количество. Очевидно, при переносе любого числа единиц по циклу равновесие между запасами и заявками не меняется: по прежнему сумма перевозок в каждой строке равна запасам этой строки, а сумма перевозок в каждом столбце - заявке этого столбца. Таким образом, при любом циклическом переносе, оставляющем перевозки неотрицательными допустимый план остаётся допустимым. Стоимость же плана при этом может меняться: увеличиваться или уменьшатся. Назовём ценой цикла увеличение стоимости перевозок при перемещении одной единицы груза по означенному циклу.
Очевидно, цена цикла ровна алгебраической сумме стоимостей, стоящих в вершинах цикла, причём стоящие в положительных вершинах берутся со знаком +, а в отрицательных со знаком -. Обозначим цену цикла через g. При перемещении одной единицы груза по циклу стоимость перевозок увеличивается на величину g. При перемещении по нему k единиц груза стоимость перевозок увеличиться на kg. Очевидно, для улучшения плана имеет смысл перемещать перевозки только по тем циклам, цена которых отрицательна.
Каждый раз, когда нам удаётся совершить такое перемещение, стоимость плана уменьшается на соответствующую величину kg. Так как перевозки не могут быть отрицательными, мы будем пользоваться только такими циклами, отрицательные вершины которых лежат в базисных клетках таблицы, где стоят положительные перевозки. Если циклов с отрицательной ценой в таблице больше не осталось, это означает, что дальнейшее улучшение плана невозможно, то есть оптимальный план достигнут. Метод последовательного улучшения плана перевозок и состоит в том, что в таблице отыскиваются циклы с отрицательной ценой, по ним перемещаются перевозки, и план улучшается до тех пор, пока циклов с отрицательной ценой уже не останется. При улучшении плана циклическими переносами, как правило, пользуются приёмом, заимствованным из симплекс-метода: при каждом шаге (цикле) заменяют одну свободную переменную на базисную, то есть заполняют одну свободную клетку и взамен того освобождают одну из базисных клеток.
При этом общее число базисных клеток остаётся неизменным и равным m + n - 1. Этот метод удобен тем, что для него легче находить подходящие циклы. Можно доказать, что для любой свободной клетке транспортной таблице всегда существует цикл и притом единственный, одна из вершин которого лежит в этой свободной клетке, а все остальные в базисных клетках. Балдаев татуировки заключенных д.с.балдаев.
Если цена такого цикла, с плюсом в свободной клетке, отрицательна, то план можно улучшить перемещением перевозок по данному циклу. Количество единиц груза k, которое можно переместить, определяется минимальным значением перевозок, стоящих в отрицательных вершинах цикла (если переместить большее число единиц груза, возникнут отрицательные перевозки). Применённый выше метод отыскания оптимального решения транспортной задачи называется распределённым; он состоит в непосредственном отыскании свободных клеток с отрицательной ценой цикла и в перемещении перевозок по этому циклу.
Распределительный метод решения транспортной задачи, с которым мы познакомились, обладает одним недостатком: нужно отыскивать циклы для всех свободных клеток и находить их цены. От этой трудоёмкой работы нас избавляет специальный метод решения транспортной задачи, который называется методом потенциалов. Решение транспортной задачи методом потенциалов Этот метод позволяет автоматически выделять циклы с отрицательной ценой и определять их цены. Пусть имеется транспортная задача с балансовыми условиями Стоимость перевозки единицы груза из A i в B j равна C ij; таблица стоимостей задана. Требуется найти план перевозок x ij, который удовлетворял бы балансовым условиям и при этом стоимость всех перевозок была минимальна. Идея метода потенциалов для решения транспортной задачи сводиться к следующему.
Представим себе что каждый из пунктов отправления A i вносит за перевозку единицы груза (всё равно куда) какую-то сумму a i; в свою очередь каждый из пунктов назначения B j также вносит за перевозку груза (куда угодно) сумму b j. Эти платежи передаются некоторому третьему лицу (“перевозчику“). Обозначим a i + b j = č ij (i=1. N) и будем называть величину č ij “псевдостоимостью' перевозки единицы груза из A i в B j. Заметим, что платежи a i и b j не обязательно должны быть положительными; не исключено, что “перевозчик' сам платит тому или другому пункту какую-то премию за перевозку.
Также надо отметить, что суммарная псевдостоимость любого допустимого плана перевозок при заданных платежах ( a i и b j) одна и та же и от плана к плану не меняется. До сих пор мы никак не связывали платежи ( a i и b j) и псевдостоимости č ij с истинными стоимостями перевозок C ij. Теперь мы установим между ними связь. Предположим, что план x ij невырожденный (число базисных клеток в таблице перевозок ровно m + n - 1).
Для всех этих клеток x ij 0. Определим платежи ( a i и b j) так, чтобы во всех базисных клетках псевдостоимости были ровны стоимостям: č ij = a i + b j = с ij, при x ij 0.
Что касается свободных клеток (где x ij = 0), то в них соотношение между псевдостоимостями и стоимостями может быть, какое угодно. Оказывается соотношение между псевдостоимостями и стоимостями в свободных клетках показывает, является ли план оптимальным или же он может быть улучшен.
Существует специальная теорема: Если для всех базисных клеток плана x ij 0,a i + b j = č ij = с ij, а для всех свободных клеток x ij =0,a i + b j = č ij ≤ с ij, то план является оптимальным и никакими способами улучшен быть не может. Нетрудно показать, что это теорема справедлива также для вырожденного плана, и некоторые из базисных переменных равны нулю. План обладающий свойством: č ij = с ij (для всех базисных клеток) (1) č ij ≤ с ij (для всех свободных клеток) (2) называется потенциальным планом, а соответствующие ему платежи ( a i и b j) - потенциалами пунктов A i и B j ( i=1.,m; j=1.,n). Пользуясь этой терминологией вышеупомянутую теорему можно сформулировать так: Всякий потенциальный план является оптимальным Итак, для решения транспортной задачи нам нужно одно - построить потенциальный план.

Оказывается его можно построить методом последовательных приближений, задаваясь сначала какой-то произвольной системой платежей, удовлетворяющей условию (1). При этом в каждой базисной клетке получиться сумма платежей, равная стоимости перевозок в данной клетке; затем, улучшая план следует одновременно менять систему платежей. Так, что они приближаются к потенциалам. При улучшении плана нам помогает следующее свойство платежей и псевдостоимостей: какова бы ни была система платежей ( a i и b j) удовлетворяющая условию (1), для каждой свободной клетки цена цикла пересчёта равна разности между стоимостью и псевдостоимостью в данной клетке: g i,j = с i,j - č i,j. Таким образом, при пользовании методом потенциалов для решения транспортной задачи отпадает наиболее трудоёмкий элемент распределительного метода: поиски циклов с отрицательной ценой. Процедура построения потенциального (оптимального) плана состоит в следующем.
В качестве первого приближения к оптимальному плану берётся любой допустимый план (например, построенный способом минимальной стоимости по строке). В этом плане m + n - 1 базисных клеток, где m - число строк, n - число столбцов транспортной таблицы. Для этого плана можно определить платежи ( a i и b j), так, чтобы в каждой базисной клетке выполнялось условие: a i + b j = с ij (3) Уравнений всего m + n - 1, а число неизвестных равно m +n.
Следовательно, одну из этих неизвестных можно задать произвольно (например, равной нулю). После этого из m + n - 1 уравнений можно найти остальные платежи a i, b j, а по ним вычислить псевдостоимости, č i,j = a i + b j для каждой свободной клетки.
ИНСТИТУТ ТРАНСПОРТА И СВЯЗИ ФАКУЛЬТЕТ КОМПЬЮТЕРНЫХ НАУК И ЭЛЕКТРОНИКИ Курсовая работа Тема: 'Решение транспортной задачи' Выполнила: Долгополова Анастасия 4902BD Рига 2010 Оглавление 1. Постановка задачи 2. Формулировка задачи 3. Теоретическое обоснование. Общие вопросы 4. Описание алгоритма нахождения потока минимальной стоимости 5. Решение индивидуального задания по шагам 6.
Программа (Mathcad) 7. Исходные данные 8. Результат программы 9. Конечные результаты Вывод 1. Постановка задачи Математическая постановка задачи. Общая постановка транспортной задачи состоит в определении оптимального плана перевозок некоторого однородного груза k-пунктов отправления а 1,а 2,а i в m пунктов назначения b 1,b 2,b j.
При этом в качестве критерия оптимальности обычно берется либо минимальная стоимость всего груза, либо минимальное время его доставки. Данная транспортная задача была рассмотрена, где в качестве критерия оптимальности была взята минимальная стоимость перевозок все груза. Были введены следующие обозначения: k - число поставщиков; m - число потребителей; i - индекс производителя i =1,к j - индекс потребителя j = 1,m а 1 - возможности i-ro производителя bj - спрос j-ro потребителя с i, j - транспортные издержки (расходы) за доставку продукции от i к j.
X i, j - объемы перевозок от i к j. Требуется составить план перевозок для которого: 1.
Все потребители удовлетворены 2. Общие транспортные расходы минимальны Требуется минимизировать функцию: Ограничения по производству: Общая сумма производимой продукции больше или равна спросу: Следовательно c i, j тарифы перевозок единицы груза из i-го пункта отправления в j-й пункт назначения, через a i - запасы груза в i-м пункте отправления, через b j - потребности в грузе в j-м пункте назначения, а через х i, j - количество единиц груза, переводимого из i-го пункта определений в j-й пункт назначения. Тогда математическая постановка транспортной задачи состоит в определении минимального значения функции. Фо рмулировка задачи Число производителей k=3 а 1=38 Объем производимой продукции а 2=45 а 3=97 Число потребителей m=4 b 1=42 b 2=35 Потребности потребителей: b 3=63 B 4=15 Производители Потребители j=1 j=2 j=3 j=4 i=1 10 11 18 32 i=2 16 14 20 25 i=3 26 28 22 30 Рис. 1 На рисунке 1 представлен исходный граф, который иллюстрирует транспортную задачу. Для решения данной задачи требуется использовать стандартную форму фиксированного источника и стока.
Каждый производитель связан с каждым потребителем. Источник не может иметь связи с потребителем, но зато каждый потребитель, в свою очередь, связан с фиктивным стоком. В обозначении дуги присутствует два параметра. Первый параметр указывает пропускную способность дуги, второй параметр показывает стоимость пересылки единицы потока на дуге. Так, например, из источника выходят дуги содержащие ограничения по пропускной способности, т.к. Данная величина характеризует производительную возможность каждого поставщика, стоимость данной дуги равна нулю, т.к.
Источник - фиксированный элемент нашего графа. Такая же ситуация обстоит с дугами, которые втекают в сток. Дуги, которые выходят из i-ых вершин (производители) и входят j-ые вершины (потребители), т.е. Соединяющие поставщика со складок, характеризуются тоже двумя параметрами. Только в этом случае, для данных дуг, в качестве первого параметра берется пропускная способность дуги равная бесконечности, а второй показатель - стоимость пересылки единицы потока. Теоретическое обоснование. Общие вопросы Сеть (транспортная сеть) - частный случай ориентированного графа.
Транспортная сеть G=( V,E) - ориентированный граф, в котором каждое ребро имеет неотрицательную пропускную способность. Выделяются две вершины: источник v и сток u такие, что любая другая вершина сети лежит на пути из v в u. V - это единственная вершина (v - источник ), которая не содержит входящих дуг, а содержит только выходящие дуги. U - это единственная вершина (u - сток), которая не содержит выходящих дуг.
Все остальные вершины - промежуточные вершины. Для любой промежуточной вершины существует путь из источника в сток. Сеть не содержит контуров. Если для сети указаны пропускные способности, то такая сеть называется транспортной сетью.
Поток - это определенная величина на дуге е. Поток в сети G=( V,E) - это функция f, заданная на дугах сети, значение на дуге е - это величина на дуге е.
Для всех промежуточных вершин соответствует сумма величин потоков на дугах входящих в вершину w, которая равна выходящему из вершины потоку. Величина потока в сети. Величина всего потока в сети модуля равна сумме величин потока выходящих из источника или сумме входящих величин потока входящих в сток. Поток минимальной стоимости - задача о потоке минимальной стоимости состоит в нахождении самого дешевого способа передачи определенного количества потока через транспортную сеть. Обозначения: Для всех дуг имеется пропускная способность: Стоимость пересылки единицы потока по дуге e: C(e) Накладываются следующие условия: 1.
Ограничение пропускной способности. Поток не может превысить пропускную способность. Поток из u в v должен быть противоположен потоку из v в u. Описание алгоритма нахожден ия потока минимальной стоимости Вход: транспортная сеть G=( V,E)с пропускной способностью дуг B(e) Выход: максимальный поток с минимальной стоимостью. Идея: Каждая итерация ставит своей целью увеличить поток в сети. Для этих целей предназначен инкрементальный граф, который позволяет увеличить поток на некоторую фиксированную величину.
Наличие прямых дуг позволяет увеличить поток на соответствующей дуге сети. Обратная дуга уменьшает поток. Алгоритм заканчивается когда в инкрементальном графе нет пути от источника к стоку. Алгоритм: Шаг 0 Данный шаг осуществляется только один раз. Вначале мы присваиваем всем дугам нулевой поток: Шаг 1 Для текущего потока строится инкрементальный граф. Прямые дуги имеются, если поток на этой дуге меньше, чем пропускная способность: Обратные дуги (дуги противоположны по отношению к ориентации прямых дуг) имеются, если на дугах имеется поток. Каждой дуге переписываем стоимость дуги.
Если е прямая, то длинна, равна стоимости пересылки, если е обратная, то ее длинна - это стоимость, но при отрицательном значении. Назначаем длины дуг для инкрементального графа: Для прямой дуги: e:C(e) Для обратной дуги: e: - C(e) Шаг 2 Нахождение кратчайшего пути в инкрементальном графе из источника v в сток u. Если такого пути нет, то происходит конец алгоритма. Найденный путь является максимальным.
Шаг 3 Нахождение минимального Д. Просматриваем дуги кратчайших путей в инкрементальном графе.
Для каждой дуги определяем величину Д. Для каждой прямой дуги: Для каждой обратной дуги: Величина, на которую можно увеличить поток. Находим минимальное значение на всех этих дугах. Шаг 4 Наращивание потока в сети. Корректируем поток на дугах в соответствии последнего пути в инкрементальном графе. На этих дугах, поток изменяется по правилам: Для прямых дуг: Для обратных дуг: Алгоритм завершается, если заданная величина потока достигнута. Переход к шагу 1.
Решение индивидуального задания по шагам Рис. Нулевой поток. Инкрементальный граф Рис. Увеличения потока в сети Рис.5. Инкрементальный граф Рис. Увеличение потока в сети Рис.7.
Инкрементальный граф Рис. Увеличение потока в сети Рис.9. Инкрементальный граф Рис. Увеличение потока в сети Рис.11. Инкрементальный граф Рис. Увеличение потока в сети Рис.13.
Инкрементальный граф Рис. Увеличение потока в сети Рис. Инкрементальный граф Рис. Увеличение потока в сети. Конец алгоритма. Программа ( Mathcad ) Исходные данные: Число вершин n=9 Очень большое число q=?
Заданная величина потока Givenflof =155 Пропускная способность дугСтоимость пересылки по дугам Где, P - поток в сети; Tekflow - текущая величина потока, Givenflofw - заданная величина потока, Vect - величина на данной дуге, L -метки 7. Результаты программы Величина потока Стоимость потока Price - стоимость 8. Конечный результат программы Данная программа была решена двумя способами: в ручную и в среде MathCad. Результаты решения обеих вариантов совпадают, значит, можно сделать вывод о том, что поставленная транспортная задача, была решена, верно.
По результатам вычислений, можно составить следующий план перевозок: Рис.